Here's a simple game that helps students cement all the different vocabulary words for the angles formed by parallel lines and transversals. I teach at school specializing in one-to-one instruction, so unfortunately it's not very much fun, but it does work! I basically just made a geometry version of my parallel and perpendicular lines game.
A journal on Teaching Math and my only hope for Professional Development
Monday, July 29, 2013
Sunday, July 21, 2013
Sharing and Laziness
My 5 year old nephew this morning had a bowl of blueberries. I had a devilish headache and was lying on my grandparent's porch swing. So when I wanted a blueberry, instead of going to get one for myself from the kitchen, I asked him if I could have one of his blueberries. He gave me three. And he fed them to me himself. Isn't sharing nice?
A few weeks ago a new teacher was hired at my school. She's certified in English, but she'll need to teach some chemistry this summer (my school is kind of crazy) so I told her I'd share all my lessons with her so that she had somewhere to start. She was surprised and thanked me and this led to a larger discussion about sharing resources. She said, and I'm quoting almost verbatim, "I'm one of those teachers who gets up Saturday morning excited to lesson plan all weekend. I'm happy to share my resources with coworkers I like, but I won't share with teachers I don't know or don't like because I don't want to encourage them to be lazy!"
A week later our school's curriculum writing team got together and our bosses told us not to make the lesson plans for the curriculum they're distributing across their various campuses too detailed. They don't want more than a page per lesson. Most of the teachers they hire aren't certified teachers because it's a private school so they told us they need a unified, regimented curriculum to support people who have never taught before. At the same time though, they said we could trust the teachers to know their subject matter and that they only needed an outline of content to be covered with no recommended instructional strategies or resources because "we don't want to stifle our teachers' creativity by giving them anything that's too detailed."
Is this a common view point held by teachers and administrators that providing rich, creative, and detailed lesson plans, activities and games promotes laziness and stifles creativity? It's hogwash! I am inspired by innovative and engaging ideas that I find in other people's lessons and the more detailed they are, the easier they are for me to adapt, to understand, or to use to help my students learn. The richer my materials, the more freedom I have to experiment. The more time I have to think about how to engage particular students. When I share my lessons I get feedback on what worked and what didn't and I become a better teacher. I can't believe how entrenched this miserly attitude is about sharing materials. This curriculum meeting was composed of dozens of teachers and administrators from all over California, New York and New Jersey and they accepted this rationale without question. That we should keep the good ideas secret to try to force other people to come up with their own good ideas. Don't they know that good ideas mate with other good ideas to produce litters of new, bouncing, energetic good ideas?
And so what if you give a lazy teacher your lesson plan. Isn't that a good thing? Those kids in the lazy teacher's classroom maybe haven't encountered innovative teaching strategies before and if a lazy teacher uses someone else's lesson plan to good effect with their students, isn't that what we all want? That even kids who have "burned out" teachers have access to rich educational experiences? Why save the good teaching just for the students who happen to have been placed in your classroom? It's so silly to hoard! I guess I can understand not wanting someone to get credit for your idea, but in the end aren't we in this business to help students learn, not to accumulate "credit" for ourselves? I'm probably way too idealistic for this world. I guess I feel so strongly about this because I wouldn't be a sixth of the teacher I am today if I hadn't ripped, stolen, copied, and adapted every idea I could skim off of other teachers' blogs and websites. So I guess I am one of the lazy teachers but boy am I a better person and a better teacher for being willing to learn from all these amazing experts surrounding me.
A few weeks ago a new teacher was hired at my school. She's certified in English, but she'll need to teach some chemistry this summer (my school is kind of crazy) so I told her I'd share all my lessons with her so that she had somewhere to start. She was surprised and thanked me and this led to a larger discussion about sharing resources. She said, and I'm quoting almost verbatim, "I'm one of those teachers who gets up Saturday morning excited to lesson plan all weekend. I'm happy to share my resources with coworkers I like, but I won't share with teachers I don't know or don't like because I don't want to encourage them to be lazy!"
A week later our school's curriculum writing team got together and our bosses told us not to make the lesson plans for the curriculum they're distributing across their various campuses too detailed. They don't want more than a page per lesson. Most of the teachers they hire aren't certified teachers because it's a private school so they told us they need a unified, regimented curriculum to support people who have never taught before. At the same time though, they said we could trust the teachers to know their subject matter and that they only needed an outline of content to be covered with no recommended instructional strategies or resources because "we don't want to stifle our teachers' creativity by giving them anything that's too detailed."
Is this a common view point held by teachers and administrators that providing rich, creative, and detailed lesson plans, activities and games promotes laziness and stifles creativity? It's hogwash! I am inspired by innovative and engaging ideas that I find in other people's lessons and the more detailed they are, the easier they are for me to adapt, to understand, or to use to help my students learn. The richer my materials, the more freedom I have to experiment. The more time I have to think about how to engage particular students. When I share my lessons I get feedback on what worked and what didn't and I become a better teacher. I can't believe how entrenched this miserly attitude is about sharing materials. This curriculum meeting was composed of dozens of teachers and administrators from all over California, New York and New Jersey and they accepted this rationale without question. That we should keep the good ideas secret to try to force other people to come up with their own good ideas. Don't they know that good ideas mate with other good ideas to produce litters of new, bouncing, energetic good ideas?
And so what if you give a lazy teacher your lesson plan. Isn't that a good thing? Those kids in the lazy teacher's classroom maybe haven't encountered innovative teaching strategies before and if a lazy teacher uses someone else's lesson plan to good effect with their students, isn't that what we all want? That even kids who have "burned out" teachers have access to rich educational experiences? Why save the good teaching just for the students who happen to have been placed in your classroom? It's so silly to hoard! I guess I can understand not wanting someone to get credit for your idea, but in the end aren't we in this business to help students learn, not to accumulate "credit" for ourselves? I'm probably way too idealistic for this world. I guess I feel so strongly about this because I wouldn't be a sixth of the teacher I am today if I hadn't ripped, stolen, copied, and adapted every idea I could skim off of other teachers' blogs and websites. So I guess I am one of the lazy teachers but boy am I a better person and a better teacher for being willing to learn from all these amazing experts surrounding me.
Monday, July 8, 2013
The Logic of Geometry
I've noticed a distinct void in the Common Core where geometric logic used to have a home. This makes me really sad for three reasons:
Below are my three logic lessons if you'd like to take a look. I'm writing lessons for the other math teachers in my school so the notes are kind of overly detailed. Also my school gives us only 50 hours a year (as opposed to the usual 150-180) to get through a year's worth of material, so it's all super condensed. I don't know if it's usable outside my school, but feel free to steal and I'd love feedback. I've uploaded the pdfs below to preserve formatting but the .docx are also available on Scribd.
Note: I borrowed some of the homework problems from Harold R. Jacob's Geometry: Seeing, doing and understanding 2nd ed. and from AMSCO's Geometry. I also totally stole the formatting from Dan Wekselgreene.
- I think it's a really great way to show students how mathematical thinking can be applied to real life
- I was skipped past geometry in high school and when I got to college, the lack of logic training was a real handicap
- And I've developed a tiny bit of skepticism about Common Core. Not a lot, but I read this article about how the Common Core was developed and it creeped me out a little. The fact that only one teacher helped develop the Common Core seems kind of terrible. I recently made friends with an economics blogger and he told me that every profession engages in "turf defending" where those in the profession reject outsiders' perspectives. That immediately made me not want to be a turf defender. I won't be the person who stomps on the school house floor and screams "MINE!" Of course I want outside input, but can I also add that it's maybe a little out of hand in education? I want to teach logic damn it!
- Oh, also, I've found logic very challenging to teach and to give up on trying to find the perfect way to introduce it now just because Common Core gives me permission feels like a cop out. (so I am pretty selfish after all.)
Below are my three logic lessons if you'd like to take a look. I'm writing lessons for the other math teachers in my school so the notes are kind of overly detailed. Also my school gives us only 50 hours a year (as opposed to the usual 150-180) to get through a year's worth of material, so it's all super condensed. I don't know if it's usable outside my school, but feel free to steal and I'd love feedback. I've uploaded the pdfs below to preserve formatting but the .docx are also available on Scribd.
Note: I borrowed some of the homework problems from Harold R. Jacob's Geometry: Seeing, doing and understanding 2nd ed. and from AMSCO's Geometry. I also totally stole the formatting from Dan Wekselgreene.
Sunday, June 30, 2013
One-to-one
My school teaches students in a one-to-one classroom; one teacher, one student. Doesn't this sound awesome? From the teaching perspective, you can customize every lesson to the student and be sure they're really learning. From the student perspective, you won't have to sit while the teacher's instruction outpaces your focus or interest.
We had an IEP meeting for one of our students and we were trying to convince the local school board that this student was making dramatic progress with us and thus his needs were being met. The moderator said "who wouldn't make progress in a one-to-one classroom!" And this got me thinking. I wouldn't. I would have HATED a one-to-one environment as a student. I didn't like to be the object of too much intense teacher concentration (and really, we can be overly intense sometimes). I liked to sit back and evaluate what the teacher said before deciding to accept or reject it. I liked to have a little freedom and control over how I took my notes and whether or not my mind drifted during class. I liked the opportunity to work with other students- our collective energy was so much more powerful than mine alone.
As a teacher, I'm not a huge fan of one-to-one either. First of all, while "classroom management" is easier (this is a pretty silly word to use for one-to-one) it can also be more difficult because there's no escaping personality conflicts. It's easier to get locked into battles of will (I avoid these like I would avoid Mexican food in NY- sorry guys, it's terrible) but I've noticed these types of intense, pride posturing battles in classrooms near mine. There are no other students near by to say "hey dude, chill out" and there's no one the teacher can turn to to exchange a sympathetic look with or to share a joke with to relieve the tension. This leads to my biggest complaint against one-to-one. It assumes that the teacher can teach all the student needs to learn. THIS ISN'T TRUE! Students learn so much more from each other. The teacher can present content and establish a respectful and fun classroom culture, but the students sustain the culture, teach each other how to act, give each other support and encouragement, joke to relieve tension, boredom or frustration, and reinterpret the content in different ways so that their classmates can see it from multiple perspectives. Learning is both a solitary and group endeavor.
So I know not many people have one-to-one classroom environments so this doesn't really matter to many besides me BUT I've been reading a little bit about the advent of personalized learning software. It seems that since the whole constructivist approach to teaching math, where everyone had to learn everything in groups, hasn't really shown huge gains, there's a movement to go in the opposite direction. Personalized learning software seems like it's going somewhere. Knewton, a personalized learning software developer based in NY, and Pearson are teaming up to bring customized, competency-based learning to as many students as possible. I think their vision of the future will be students sitting at home, in coffee shops, in libraries or even in classrooms, logging in to their program and getting a wholly customized learning experience. The Knewton software amasses student data and has an algorithm that decides when a student is ready to move on to new material, and what that new material will be. This is exactly like what I'm doing right now, except without the teacher.
Here's what I see happening:
We had an IEP meeting for one of our students and we were trying to convince the local school board that this student was making dramatic progress with us and thus his needs were being met. The moderator said "who wouldn't make progress in a one-to-one classroom!" And this got me thinking. I wouldn't. I would have HATED a one-to-one environment as a student. I didn't like to be the object of too much intense teacher concentration (and really, we can be overly intense sometimes). I liked to sit back and evaluate what the teacher said before deciding to accept or reject it. I liked to have a little freedom and control over how I took my notes and whether or not my mind drifted during class. I liked the opportunity to work with other students- our collective energy was so much more powerful than mine alone.
As a teacher, I'm not a huge fan of one-to-one either. First of all, while "classroom management" is easier (this is a pretty silly word to use for one-to-one) it can also be more difficult because there's no escaping personality conflicts. It's easier to get locked into battles of will (I avoid these like I would avoid Mexican food in NY- sorry guys, it's terrible) but I've noticed these types of intense, pride posturing battles in classrooms near mine. There are no other students near by to say "hey dude, chill out" and there's no one the teacher can turn to to exchange a sympathetic look with or to share a joke with to relieve the tension. This leads to my biggest complaint against one-to-one. It assumes that the teacher can teach all the student needs to learn. THIS ISN'T TRUE! Students learn so much more from each other. The teacher can present content and establish a respectful and fun classroom culture, but the students sustain the culture, teach each other how to act, give each other support and encouragement, joke to relieve tension, boredom or frustration, and reinterpret the content in different ways so that their classmates can see it from multiple perspectives. Learning is both a solitary and group endeavor.
So I know not many people have one-to-one classroom environments so this doesn't really matter to many besides me BUT I've been reading a little bit about the advent of personalized learning software. It seems that since the whole constructivist approach to teaching math, where everyone had to learn everything in groups, hasn't really shown huge gains, there's a movement to go in the opposite direction. Personalized learning software seems like it's going somewhere. Knewton, a personalized learning software developer based in NY, and Pearson are teaming up to bring customized, competency-based learning to as many students as possible. I think their vision of the future will be students sitting at home, in coffee shops, in libraries or even in classrooms, logging in to their program and getting a wholly customized learning experience. The Knewton software amasses student data and has an algorithm that decides when a student is ready to move on to new material, and what that new material will be. This is exactly like what I'm doing right now, except without the teacher.
Here's what I see happening:
- computers probably aren't smart enough to do this yet. I don't know if they ever will be. I have an Algebra student who asked me if numbers go on forever. We had a nice side discussion on the nature of number and infinity which he understood. His abstract reasoning capabilities have far outpaced his computational competence so he asks really good, deep math questions and understands the answers even when he struggles with adding fractions. I can satisfy his deeper curiosity while still drilling him on basic arithmetic. A program would decide that he's not ready for anything beyond basic computation.
- I do believe that school is about more than learning content. I think that learning to work cooperatively is important. Learning to share a joke to relieve stress is important. Learning how to speak up for yourself to an authority figure is important. Socialization is important. Maybe this just makes me old fashioned. But having people by your side makes learning more fun too.
- Peers push you to accomplish more than you can by yourself. This is a problem I've seen in one-to-one teaching- that it's so much harder to motivate a student to study independently or to work on projects. When there's no one to share it with, no peer audience, teenagers shut down and disengage. Duh! Even teenagers with special needs (we teach a lot of students with severe social anxiety) need peers to support them. Even if you place kids in the same classrooms to use these educational technologies, they won't be learning the same content so won't be able to support or motivate each other effectively.
- Finally, if you allow students to do the work at home, I think cheating will become the norm. I think it already is. A coworker of mine (a teacher!) admitted to me that she takes all of her sisters' online tests for her because her sister is an athlete and doesn't need school.
Can't we find a middle ground? There is never going to be one model that works for everyone, but we all deserve to experience different types of learning. I may not like one-to-one learning because it makes me uncomfortable, but I went in to see my professors to get help on papers and it was good for me. We all need a mix of different experiences. We need technology and classrooms and individualized instruction and games and textbooks and teachers. Why can't technology make our classrooms richer and more full of different kinds of learning? Why is it a choice between classrooms or personalized learning? Can't we recognized that there are good things about classrooms? Why are we so obsessed with "or"? Why not and? Knewton and Pearson might say though that they are offering an "and" option. That this is meant to enrich teachers' curricula not replace them, but I'm suspicious that this is just another way to devalue teachers' professionalism. I read an article in Newsweek (I think but of course I can't find it now) where the head of one of these personalized software companies admitted that he didn't employ any educators on staff. And Pearson, based on what I've seen of their textbooks, doesn't know that much about teaching either.
Saturday, February 2, 2013
Logarithm Dominoes
I'm currently planning my pre-calc unit on logarithms and I just can't seem to find enough fun ways to drill logarithms. It really is just about practice I think, but I HATE giving students worksheets full of problems. I groan every time I see a Kuta software worksheet. I know that games basically just do the same thing in a dressed up form, but at least there's a measure of competition or strategy that gives students a focus. I just read Amy Gruen's post on practicing logarithms and almost threw out some expletives because I saw her link to logarithm dominoes and I spent a nice chunk of time last weekend to making my own logarithm dominoes. Its both wonderful and incredibly frustrating to spend hours on something then find that someone got there first and did it better. At least you know your idea was good, but you could have saved yourself so much time! (this happened to me last year with Kate Nowak's logarithm laws worksheet . I'd made one for myself then stumbled upon hers and hers was so much better!) But fortunately for me, Amy Gruen's logarithm dominoes are very different from mine, so I thought I'd share what I came up with.
I threw together the following logarithm property dominoes. I haven't had a chance to try them out yet, so I'm not sure the ratios are correct. But I figured it was a start and I don't know when I'll have the initiative or time to post them again. Here are the dominoes:
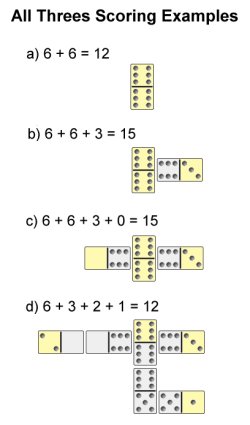
You should be able to play any domino game with these cards that you want but I planned to play the game "all threes". Here are the rules:
I threw together the following logarithm property dominoes. I haven't had a chance to try them out yet, so I'm not sure the ratios are correct. But I figured it was a start and I don't know when I'll have the initiative or time to post them again. Here are the dominoes:
You should be able to play any domino game with these cards that you want but I planned to play the game "all threes". Here are the rules:
- Each player draws 5 dominoes. You start by playing a double domino (one end equals the same number as the other end: 2-2 for example)
- You can build off the double domino in 4 directions- above, down, left and right. To play off a domino, you must match ends that have the same value.
- Players take turns placing dominoes.
- If a player can’t place a domino, they must draw more dominoes until they can play.
- After each player places a domino, count up the total of all loose ends. If the total is a multiple of 3, the player gets that many points.
- The game ends when either a player runs out of dominoes in their hand or when a player reaches 100 points. If a player runs out of dominoes in their hand, the player with the most points wins.
Since these are logarithm expressions and not straight forward pips, players must make the conversions in their
head or on paper.
Now I just need to figure out a fun way to teach solving logarithm and exponential equations....
Labels:
dominoes,
games,
logarithm properties,
logarithms,
Pre-calculus
Sunday, December 30, 2012
Sometimes Teaching is the BEST Job in the World
I received this message today from a student I taught for 3 years back in Oregon.
I wanted to thank you. Even though you are not my teacher anymore, you still help me all the time. You wrote in my yearbook to remember that I am good at math, and I always go back to that and it actually helps me when I am stressed about algebra. Whenever I think about it, I feel as though I can push through and actually do it. I am doing pretty well in it so far and I owe part of that to you.
Sometimes teaching is the best job in the world.
I wanted to thank you. Even though you are not my teacher anymore, you still help me all the time. You wrote in my yearbook to remember that I am good at math, and I always go back to that and it actually helps me when I am stressed about algebra. Whenever I think about it, I feel as though I can push through and actually do it. I am doing pretty well in it so far and I owe part of that to you.
Sometimes teaching is the best job in the world.
Wednesday, December 19, 2012
Common Core vs. Regents?
This being my first year teaching in New York, navigating the Regents has been a challenge. I feel so torn in different directions that I've ended up in a state of complete and utter indecision. Especially about geometry. Here are the facts:
- I'm teaching at a private school so technically, we don't have to do the Regents but our parents want us to offer Regents prep courses.
- The private school has its own curriculum imported from its California model that isn't correlated either to New York State or to the Common Core.
- We are restricted to 50 total sessions with the students per year rather than the 150 classroom hours you normally get at public school. If we need to go over 50, the parents have to pay more so we try very hard not to do that.
- I love all the ideas the blogging community has for geometry, but everyone seems to be pushing Common Core and the geometry Regents exam doesn't seem to be there yet.
- I have my own inclinations for teaching geometry that I'm having trouble shoving to the side to adhere to any standards.
- Two months ago my boss asked me to look at our boxed curriculum from California and compare it to the New York State Standards and the Regents exam and make sure they were aligned. I discovered that they couldn't be more different and she has asked me to come up with a Regents friendly curriculum map.
I LOVE the way Drawing on Math has organized her geometry class, but I'm really torn. I was also very inclined to do parallel lines and transverals right at the beginning but a Regents aligned textbook, AMSCO-Geometry, puts it more than half-way through the course. Why did they make this decision? Is there some profound reason students should do congruent triangles and transformations first? They've split up all the points of concurrency in triangles into different chapters too, whereas I was inclined to put them all together. Which way is best? A lot of the organization seems strange to me, but I've only learned geometry through teaching it over the past two years (I was skipped through it in High School and my college didn't offer any college level geometry courses) and I'm unsure whether or not to trust myself on what seems logical to me vs. how the book organizes material.
In the same Drawing on Math post, she also mentions scrapping most of the logic unit and only teaching converses. But the NYS standards have LOTS of logic material including converses, negations, contrapositives, direct and indirect proofs, truth tables and Law of Detachment. BUT, combing through old Regents exams reveals that they only ever seem to ask questions about negations, and the Common Core doesn't have much logic at all... Yet I love teaching it and when I got to college and took college level math courses, the fact that I'd been skipped through geometry became a real handicap in the more advanced proof based classes because I'd never been exposed to logic before. So I'm inclined to teach logic because knowing just high school level geo-logic would have really helped me. BUT we only have 50 sessions and I can't waste time on material not on the Regents exam. BUT everyone's saying the Common Core is better anyway so shouldn't I align our curriculum to the Common core and not to a standardized test? BUT our kids need to pass the Regents because our parents care about it so much.
My heart tells me that I should just teach it in a way that feels right to me and if the kids really internalize the material they will pass the Regents. Yet the Regents has such specific types of questions covering specific topics that I'm worried if I don't teach them with the Regents in mind, they'll get to the exam and it will use vocabulary they're not used to and ask types of questions we haven't covered. I wish the State would just trust me a little. I can help the students navigate this material but I want to let them enjoy it and I want to let them explore and I feel like I can't do that with this ticking bomb hanging over my head. I guess I just have to try something and hope. Teaching is about experimenting however nervous this makes me. I hate the idea of an experiment failing at the detriment to a student's enjoyment of math. But we learn by making mistakes right?
[12/20/12 edited to add the following paragraph] I'm still struggling with the geo curriculum and I decided to trust the book and do triangles before parallel lines and transverals but I'm running into difficulties. If you don't do parallel lines and transversals first, then you can't do the proof that there are 180 degrees in a triangle (or at least you can't do my favorite one) and trying to do all the triangle stuff without this is pretty crippling. In fact talking about angles at all becomes a little sticky. We're supposed to do exterior angles in the triangle unit, but how do you prove any of the exterior angle theorems without knowing there are 180 degrees in a triangle? And what about AAS triangle congruence? They've thrown that in much later in the course 3 units after doing all the other triangle congruence theorems. I wish textbooks provided a justification for how they organize their content because I always start by trying to follow a book (they know best right? Tons of experts and trials in classrooms and thousands of dollars.) and then always scrap the book a quarter of the way in because their sequencing just doesn't make sense to me. I wish I could squelch my internal sense of logic and just trust a textbook... my life would be so much easier.
[12/20/12 edited to add the following paragraph] I'm still struggling with the geo curriculum and I decided to trust the book and do triangles before parallel lines and transverals but I'm running into difficulties. If you don't do parallel lines and transversals first, then you can't do the proof that there are 180 degrees in a triangle (or at least you can't do my favorite one) and trying to do all the triangle stuff without this is pretty crippling. In fact talking about angles at all becomes a little sticky. We're supposed to do exterior angles in the triangle unit, but how do you prove any of the exterior angle theorems without knowing there are 180 degrees in a triangle? And what about AAS triangle congruence? They've thrown that in much later in the course 3 units after doing all the other triangle congruence theorems. I wish textbooks provided a justification for how they organize their content because I always start by trying to follow a book (they know best right? Tons of experts and trials in classrooms and thousands of dollars.) and then always scrap the book a quarter of the way in because their sequencing just doesn't make sense to me. I wish I could squelch my internal sense of logic and just trust a textbook... my life would be so much easier.
Subscribe to:
Posts (Atom)