Soo.... I wrote an article for Quartz magazine on why so many people identify themselves as "math people" or "non math people" and what we can do about it. It's the first time I've ever been officially published and I'm both terrified and excited. The magazine editors came up with the article title and the subheadings but the rest is mostly my work. Here it is.
I don't know how many people will read it, but so far it's been well worth the two weeks I stressed over it because of some of the wonderful responses I've gotten from former students. I have to share them. If the article was terrible, it was worth writing just to get these wonderful words of encouragement from my students.
Student 1: Congratulations on having your article published! I miss having you as my teacher so much! You were the best teacher I have ever had <3
Student 2: You are so brilliant! I am so lucky I had you as my teacher. Not only were you a good teacher, but a super-cool one. I miss you!
Student 3 (this is the one that made me cry): I want to thank you for writing that article. I have been so scared to take another math class because of the last one I took. It was Math 110; basic college Algebra. I failed the class. I went to the math lab regularly, I participated in study groups, office hours, the works. I tried hard, but the teacher just could not explain things in a way that I could understand well and remember. After that class, I decided that I could not ever have a career in the math/science field despite my love for them because I just was not a "math person." A few weeks ago I was reading a Biology/Science textbook and realized that those were the only textbooks I had ever read for fun. I always have. But right then I nearly started crying thinking about how I just did not have the math skills to ever pursue it. Your article has given me hope... I now have the courage to try again. Thank you so much. I am so grateful for the time I had as your student. I know that all of your former students feel the same way. We love you. You are the best. Don't believe anyone who tells you otherwise
A journal on Teaching Math and my only hope for Professional Development
Sunday, December 1, 2013
Saturday, November 30, 2013
Why teach Algebra
I've been thinking about a response to the article published in the New York Times, "Is Algebra Necessary?" for over a year. I've started maybe 10 different draft posts and scrapped them. I've been following the follow-up debates in blogs (see Wiggins' post on algebra 1 as a poorly designed course and Honner's response to Wiggins) and thinking about related articles like "Wrong Answer: The Case Against Algebra II" and "The Mathematician's Lament".
I've been so torn about how to respond because as a math teacher, of course I believe teaching math is vital. I became a teacher because I wanted to save the world and martyr myself with 80 hour work weeks and panicked sweats every Sunday night. And reading these articles seems to trivialize what I have poured sweat, tears and many many gallons of coffee into. Yet I see their side of things. I hate the idea of algebra 1 being the barrier between a talented artist and a career in art. I am now teaching students in algebra 1 who have failed it two or three times before and it broke my heart yesterday when I handed back a homework assignment I had given a 7/10 to a student and her face lit up as she said that she'd never gotten a passing score on a math assignment.
Also, I've never used math in "the real world". I'm not an engineer, an economist, a physicist or a banker. I don't know how math gets used out there so who am I to tell students year after year that they're going to need these skills when I don't know that they will. The argument that math sharpens general cognitive skills and teaches students problem solving strategies that will be useful later in life, especially as it's backed up by research, holds water but that doesn't help us algebra teachers argue for teaching algebra. Why not teach statistics? Or a formal logic class? Should we defend the traditional math sequence, or should we branch out and give students who are failing at algebra alternative math options?
But the other day I was talking with my husband and I realized why I love math, not why I teach it or how I use it, but why I love it. And I think the reason for my love is also the reason it needs to be taught. I am decidedly introverted, perhaps the queen of introverts. I can't handle phones- it's very very difficult for me to talk on the phone with those I love and even harder with those I don't know. I need to see eyes, to gauge reactions, to be able to comment on surroundings or engage my conversation partner in a task that removes the focus of conversation off of me. I've found the adult world intimidating and overwhelming and need frequent breaks from it. I like playing board games to escape because they have defined protocols. I know exactly what the object of the game is and how to get there. I can enjoy socializing while playing because of the game's comforting structure.
The world is overwhelming for anyone- even those not so introverted as I am. There are complex political systems to understand, the natural world can be scary and confusing, bad things happen to good people inexplicably, we are born with deficiencies and insecurities that make socializing difficult or awkward. School is for this- to help our young students learn that knowledge will conquer their confusions and difficulties. When they understand how something works, they aren't as afraid of it and they know how to navigate it. Or when they understand how something works, they won't make a mess of it because of overconfidence or arrogance. Understanding our history and political systems is vital but impossible. We give our students the best analysis tools we can and hope that time and a love of learning will help guide them in making wise decisions for themselves. Learning science is fascinating and practical, but requires lots of field trips, labs, props and math to even begin understanding the basics of how our world works. Math is the only field where understanding can be created by the student with nothing more than a pencil, a paper and a system of logical rules- just like a board game. Yet unlike a board game, math helps us untangle the mysteries of how the world around us works. It gives us a sense of order and control over our own minds and our own environments. Isn't our job as educators to help students make sense of the world around them and to help them feel in control of their own lives? Math is instrumental in accomplishing these two goals but especially for helping students realize what their minds are capable of and that they don't have to go outside to conquer a small piece of their universe.
So this is why we need algebra and not just statistics or logic. Algebra is about finding the unknowns. It's about looking at how the complex variables in our lives that affect each other and us. It has the further advantage of being the bedrock of higher level math so that if a student chose to pursue advanced math, she could. It's got an easily understood framework of logic so that when the basic properties of algebra are mastered, all the other results are easily provable by a 14 year old with a pencil. But most importantly, mastering algebra - especially because it can be such a difficult transition for many students- makes a student feel powerful and in control of her mind and world. Isn't this how we want students to feel when they go out to help shape our society?
I've been so torn about how to respond because as a math teacher, of course I believe teaching math is vital. I became a teacher because I wanted to save the world and martyr myself with 80 hour work weeks and panicked sweats every Sunday night. And reading these articles seems to trivialize what I have poured sweat, tears and many many gallons of coffee into. Yet I see their side of things. I hate the idea of algebra 1 being the barrier between a talented artist and a career in art. I am now teaching students in algebra 1 who have failed it two or three times before and it broke my heart yesterday when I handed back a homework assignment I had given a 7/10 to a student and her face lit up as she said that she'd never gotten a passing score on a math assignment.
Also, I've never used math in "the real world". I'm not an engineer, an economist, a physicist or a banker. I don't know how math gets used out there so who am I to tell students year after year that they're going to need these skills when I don't know that they will. The argument that math sharpens general cognitive skills and teaches students problem solving strategies that will be useful later in life, especially as it's backed up by research, holds water but that doesn't help us algebra teachers argue for teaching algebra. Why not teach statistics? Or a formal logic class? Should we defend the traditional math sequence, or should we branch out and give students who are failing at algebra alternative math options?
But the other day I was talking with my husband and I realized why I love math, not why I teach it or how I use it, but why I love it. And I think the reason for my love is also the reason it needs to be taught. I am decidedly introverted, perhaps the queen of introverts. I can't handle phones- it's very very difficult for me to talk on the phone with those I love and even harder with those I don't know. I need to see eyes, to gauge reactions, to be able to comment on surroundings or engage my conversation partner in a task that removes the focus of conversation off of me. I've found the adult world intimidating and overwhelming and need frequent breaks from it. I like playing board games to escape because they have defined protocols. I know exactly what the object of the game is and how to get there. I can enjoy socializing while playing because of the game's comforting structure.
The world is overwhelming for anyone- even those not so introverted as I am. There are complex political systems to understand, the natural world can be scary and confusing, bad things happen to good people inexplicably, we are born with deficiencies and insecurities that make socializing difficult or awkward. School is for this- to help our young students learn that knowledge will conquer their confusions and difficulties. When they understand how something works, they aren't as afraid of it and they know how to navigate it. Or when they understand how something works, they won't make a mess of it because of overconfidence or arrogance. Understanding our history and political systems is vital but impossible. We give our students the best analysis tools we can and hope that time and a love of learning will help guide them in making wise decisions for themselves. Learning science is fascinating and practical, but requires lots of field trips, labs, props and math to even begin understanding the basics of how our world works. Math is the only field where understanding can be created by the student with nothing more than a pencil, a paper and a system of logical rules- just like a board game. Yet unlike a board game, math helps us untangle the mysteries of how the world around us works. It gives us a sense of order and control over our own minds and our own environments. Isn't our job as educators to help students make sense of the world around them and to help them feel in control of their own lives? Math is instrumental in accomplishing these two goals but especially for helping students realize what their minds are capable of and that they don't have to go outside to conquer a small piece of their universe.
So this is why we need algebra and not just statistics or logic. Algebra is about finding the unknowns. It's about looking at how the complex variables in our lives that affect each other and us. It has the further advantage of being the bedrock of higher level math so that if a student chose to pursue advanced math, she could. It's got an easily understood framework of logic so that when the basic properties of algebra are mastered, all the other results are easily provable by a 14 year old with a pencil. But most importantly, mastering algebra - especially because it can be such a difficult transition for many students- makes a student feel powerful and in control of her mind and world. Isn't this how we want students to feel when they go out to help shape our society?
Sunday, November 17, 2013
Congruent Triangles Review Game
I played a review game with my geometry class a few weeks ago that they loved so I thought I'd share it. I think I stole this idea from a blog, but I can't for the life of me remember which blog, so if it's yours let me know.
I stole the problems from the Pearson Geometry Common Core Edition.
I printed the document below double sided but didn't staple it. Then I shuffled the pages and made 8 or so copies of all of them for the 8 groups in my class. The groups needed to start with the page that has "RP" at the top and do the proof. Then they hunt for the answer in the sheaf of papers. When they find the answer, they grade their proof against the answer key, turn the answer key over and work the problem on the back of the answer key. Then they hunt out the answer key to the new problem.
If they keep track of the order in which they did the problems, they can write down all the letters from the upper right hand corners of the problems, unscramble them and a message appears.
I had students for the first time actually paying close attention to every step of the proof, asking great questions about why different steps appeared, if they were necessary, and if/how order in the proof matters. They also really loved working out the code.
I know it's just drill and kill two-column proofing, but it did a nice job of getting my students to compare different proving methods and getting them to analyze their own work.
Here it is:
I stole the problems from the Pearson Geometry Common Core Edition.
I printed the document below double sided but didn't staple it. Then I shuffled the pages and made 8 or so copies of all of them for the 8 groups in my class. The groups needed to start with the page that has "RP" at the top and do the proof. Then they hunt for the answer in the sheaf of papers. When they find the answer, they grade their proof against the answer key, turn the answer key over and work the problem on the back of the answer key. Then they hunt out the answer key to the new problem.
If they keep track of the order in which they did the problems, they can write down all the letters from the upper right hand corners of the problems, unscramble them and a message appears.
I had students for the first time actually paying close attention to every step of the proof, asking great questions about why different steps appeared, if they were necessary, and if/how order in the proof matters. They also really loved working out the code.
I know it's just drill and kill two-column proofing, but it did a nice job of getting my students to compare different proving methods and getting them to analyze their own work.
Here it is:
Sunday, November 3, 2013
Awesome Article
Here's an AWESOME article on that oft heard phase that crushes teachers' souls, "I'm not a math person." It's titled "Miles Kimball and Noah Smith on the fallacy of inborn math ability."
Sunday, October 13, 2013
I'm a real teacher again!
My life has kind of been in turmoil for a while. After one cross country move last year, we've just driven back across the country. By car: Oregon-> New York-> California. By airplane: DC, Japan, Indiana, Ohio, and Arizona (and Oregon and New York a bunch). This is all in a 12 month time period. I wonder how many miles I've traveled. I think it's probably close to a world record.
I'm also undergoing the teacher licensing process in my 4th state! Woot! Soon I'll collect all 50 :). I would totally go for national board certification, but I'm not wise enough or anywhere consistent enough to go for that yet.
We moved back to the west coast in September because of a family illness. I left my job at the one-to-one private school abruptly and was actually looking forward to some time off. The private school was year-round so I was getting pretty tired. But of course, obsessive compulsive me couldn't stop checking craigslist and within 24 hours of arriving in San Diego I had a job interview at a charter school. I was really really nervous about not having a job plan when we decided to come spend some time in California so I was delighted at the prospect of a job so quickly. But it's in a classroom again with a lot of kids and I start tomorrow and I'm terrified.
It's been a year since I worked in a classroom with more than one student and my pitiful classroom management skills have completely atrophied plus my obsessive compulsive work ethic already has me fruitlessly planning lesson after lesson even though I have no idea where the kids are and will have to scrap all this work and start over.
Do the nerves ever go away? I wish they would. Everyone says I'm super lucky to have landed a job in late September/early October but right now I wish I could go back two weeks and kick my over eager, initiative grabbing, hopeful self and tell her to just CHILL!
But I am happy to be teaching in a classroom again, I am. And I will try to post more because now I'm legitimate.
I'm also undergoing the teacher licensing process in my 4th state! Woot! Soon I'll collect all 50 :). I would totally go for national board certification, but I'm not wise enough or anywhere consistent enough to go for that yet.
We moved back to the west coast in September because of a family illness. I left my job at the one-to-one private school abruptly and was actually looking forward to some time off. The private school was year-round so I was getting pretty tired. But of course, obsessive compulsive me couldn't stop checking craigslist and within 24 hours of arriving in San Diego I had a job interview at a charter school. I was really really nervous about not having a job plan when we decided to come spend some time in California so I was delighted at the prospect of a job so quickly. But it's in a classroom again with a lot of kids and I start tomorrow and I'm terrified.
It's been a year since I worked in a classroom with more than one student and my pitiful classroom management skills have completely atrophied plus my obsessive compulsive work ethic already has me fruitlessly planning lesson after lesson even though I have no idea where the kids are and will have to scrap all this work and start over.
Do the nerves ever go away? I wish they would. Everyone says I'm super lucky to have landed a job in late September/early October but right now I wish I could go back two weeks and kick my over eager, initiative grabbing, hopeful self and tell her to just CHILL!
But I am happy to be teaching in a classroom again, I am. And I will try to post more because now I'm legitimate.
Saturday, August 31, 2013
Exponent Rules GAME
I've posted on this topic a bunch of times here, here and here, but I'm not tired yet of hammering more nails into this coffin. I think that correctly mastering exponent rules is a gateway skill. Maybe one of the most important gateway skills in algebra. Exponent rules:
- Formalize the meaning of multiplication and division for algebra.
- Provide the first forum for students to effectively use reducing in an algebraic context.
- Introduces students for the first time to how simple algebra definitions (i.e. the definition of an exponent) can be used to prove a multitude of other cool rules that make doing math easier. In other words exponent rules formalize the structure of mathematical logic and proof for students.
- Is often the first time students see and manipulate algebraic rules represented purely with variables. If students can understand and use exponent rules, it prepares them for using and understanding other rules represented with abstract mathematical language.
- Set the foundation for a student's understanding of polynomial functions, radical functions, exponential functions, and logarithmic functions. Without a solid understanding of exponents and their properties students will struggle with all of these types of functions later.
And I think we can teach the exponent rules well because they're just not that hard to derive, but the level of abstraction is what makes it difficult for students. So in teaching exponent rules, I believe we should focus on teaching students the abstraction, and the rules get learned along the way.
That being said, I don't know how to do it but I keep trying. I've updated my lesson on developing the exponent rules. You can find that here and also, I've developed a simple game that I hope helps students cement the rules and learn to play with them. The game involves both strategy, luck and understanding of exponents so I think it's pretty good but it's only had a few trial runs.
Materials: You'll need a set of blue cards and a set of green cards. You can download the cards and the rules here. Lay the cards out like so:
Materials: You'll need a set of blue cards and a set of green cards. You can download the cards and the rules here. Lay the cards out like so:
Object: Combine
your starting expression with green cards to create the target expression.
Rules:
(1) You
may use as many green cards as you wish.
(2) Cards
that look like this: ( )^2 must be applied to your whole expression so far. So if you start with the card “ab" and you grab the green card ( )^2 you will end up with a^2 b^2
(3) If
neither player can find the right cards to create the target expression, three
more green cards can be put down.
(4) Once
the target expression is reached by a player, that player gets the blue card and all the green cards they used to make
the winning expression. A new blue
card is then put down and green cards are added until there are 9 green cards again.
(5) Once all the green cards are gone, the game is
ended and the player with the most green and blue cards wins.
Examples:
Here are several examples of how the players in the set-up above could reach the target expression.
Labels:
algebra 1,
exponent game,
exponent rules,
pre-algebra
Saturday, August 3, 2013
Not Ratios again!
Students either seem to "get" ratios or they don't. I don't know what to do about it. I made a really detailed ratio and proportion lesson based on beats per minute and the fastest guitar player in the world for my algebra 1 students. 3 students that I used it on loved it and understood everything just fine, 1 student could not get it no matter what I tried.
I drew a picture of a person and said that he was 6 ft tall but a shrink-ray shrunk him to 2 ft. If his legs were 3 ft long originally how long are they now? My student thought for a second and then said "-1 feet?" I tried pictures of triangles, I tried explaining that scale factors worked with multiplication and division, not addition and subtraction, I tried just showing him the math steps based on fractions in a last ditch attempt to get him to walk out of the class with something. But none of it worked because he didn't have an internal sense for proportion. He could do the mechanism of cross-multiplication, but a "sense" for proportion just eluded him.
I'm now working on a lesson for geometry introducing ratio and proportion and I'm getting a little cold and clammy because I have nothing. My experience is just kids see it or they don't and if they don't, I don't know what to do. Sheer perseverance and drill have helped these students eventually reach an "aha" moment, but it just seems to be based on time, not on cleverness of the activity (or I haven't found or thought of a sufficiently clever activity.) I've been sitting in a coffee shop for an hour now and so far, I just have a warm-up:
Update [8/4/2013] Here's the lesson I eventually came up with. I think it does a decent job.
And here's an "I notice, I wonder" activity that could be used to get students thinking about ratio and proportion. Both of these are PDFs to preserve formatting, but if you go to my scribd profile you can find the .docx versions.
I drew a picture of a person and said that he was 6 ft tall but a shrink-ray shrunk him to 2 ft. If his legs were 3 ft long originally how long are they now? My student thought for a second and then said "-1 feet?" I tried pictures of triangles, I tried explaining that scale factors worked with multiplication and division, not addition and subtraction, I tried just showing him the math steps based on fractions in a last ditch attempt to get him to walk out of the class with something. But none of it worked because he didn't have an internal sense for proportion. He could do the mechanism of cross-multiplication, but a "sense" for proportion just eluded him.
I'm now working on a lesson for geometry introducing ratio and proportion and I'm getting a little cold and clammy because I have nothing. My experience is just kids see it or they don't and if they don't, I don't know what to do. Sheer perseverance and drill have helped these students eventually reach an "aha" moment, but it just seems to be based on time, not on cleverness of the activity (or I haven't found or thought of a sufficiently clever activity.) I've been sitting in a coffee shop for an hour now and so far, I just have a warm-up:
- Which pair of numbers is out of place? Explain why you chose that pair.
- 3 and 4
- 5 and 6
- 9 and 12
- 27 and 36
- Which pair of numbers is out of place? Explain why you chose that pair.
- 9 and 12
- 12 and 15
- 20 and 25
- 32 and 40
- You got a part time job at The Pizza Hub. You just found out that your co-worker makes more money. Which statement would make you angrier? Why?
- Your coworker makes $10 more than you.
- Your coworker makes double what you make.
Update [8/4/2013] Here's the lesson I eventually came up with. I think it does a decent job.
And here's an "I notice, I wonder" activity that could be used to get students thinking about ratio and proportion. Both of these are PDFs to preserve formatting, but if you go to my scribd profile you can find the .docx versions.
Monday, July 29, 2013
Parallel Lines and Transversals game
Here's a simple game that helps students cement all the different vocabulary words for the angles formed by parallel lines and transversals. I teach at school specializing in one-to-one instruction, so unfortunately it's not very much fun, but it does work! I basically just made a geometry version of my parallel and perpendicular lines game.
Sunday, July 21, 2013
Sharing and Laziness
My 5 year old nephew this morning had a bowl of blueberries. I had a devilish headache and was lying on my grandparent's porch swing. So when I wanted a blueberry, instead of going to get one for myself from the kitchen, I asked him if I could have one of his blueberries. He gave me three. And he fed them to me himself. Isn't sharing nice?
A few weeks ago a new teacher was hired at my school. She's certified in English, but she'll need to teach some chemistry this summer (my school is kind of crazy) so I told her I'd share all my lessons with her so that she had somewhere to start. She was surprised and thanked me and this led to a larger discussion about sharing resources. She said, and I'm quoting almost verbatim, "I'm one of those teachers who gets up Saturday morning excited to lesson plan all weekend. I'm happy to share my resources with coworkers I like, but I won't share with teachers I don't know or don't like because I don't want to encourage them to be lazy!"
A week later our school's curriculum writing team got together and our bosses told us not to make the lesson plans for the curriculum they're distributing across their various campuses too detailed. They don't want more than a page per lesson. Most of the teachers they hire aren't certified teachers because it's a private school so they told us they need a unified, regimented curriculum to support people who have never taught before. At the same time though, they said we could trust the teachers to know their subject matter and that they only needed an outline of content to be covered with no recommended instructional strategies or resources because "we don't want to stifle our teachers' creativity by giving them anything that's too detailed."
Is this a common view point held by teachers and administrators that providing rich, creative, and detailed lesson plans, activities and games promotes laziness and stifles creativity? It's hogwash! I am inspired by innovative and engaging ideas that I find in other people's lessons and the more detailed they are, the easier they are for me to adapt, to understand, or to use to help my students learn. The richer my materials, the more freedom I have to experiment. The more time I have to think about how to engage particular students. When I share my lessons I get feedback on what worked and what didn't and I become a better teacher. I can't believe how entrenched this miserly attitude is about sharing materials. This curriculum meeting was composed of dozens of teachers and administrators from all over California, New York and New Jersey and they accepted this rationale without question. That we should keep the good ideas secret to try to force other people to come up with their own good ideas. Don't they know that good ideas mate with other good ideas to produce litters of new, bouncing, energetic good ideas?
And so what if you give a lazy teacher your lesson plan. Isn't that a good thing? Those kids in the lazy teacher's classroom maybe haven't encountered innovative teaching strategies before and if a lazy teacher uses someone else's lesson plan to good effect with their students, isn't that what we all want? That even kids who have "burned out" teachers have access to rich educational experiences? Why save the good teaching just for the students who happen to have been placed in your classroom? It's so silly to hoard! I guess I can understand not wanting someone to get credit for your idea, but in the end aren't we in this business to help students learn, not to accumulate "credit" for ourselves? I'm probably way too idealistic for this world. I guess I feel so strongly about this because I wouldn't be a sixth of the teacher I am today if I hadn't ripped, stolen, copied, and adapted every idea I could skim off of other teachers' blogs and websites. So I guess I am one of the lazy teachers but boy am I a better person and a better teacher for being willing to learn from all these amazing experts surrounding me.
A few weeks ago a new teacher was hired at my school. She's certified in English, but she'll need to teach some chemistry this summer (my school is kind of crazy) so I told her I'd share all my lessons with her so that she had somewhere to start. She was surprised and thanked me and this led to a larger discussion about sharing resources. She said, and I'm quoting almost verbatim, "I'm one of those teachers who gets up Saturday morning excited to lesson plan all weekend. I'm happy to share my resources with coworkers I like, but I won't share with teachers I don't know or don't like because I don't want to encourage them to be lazy!"
A week later our school's curriculum writing team got together and our bosses told us not to make the lesson plans for the curriculum they're distributing across their various campuses too detailed. They don't want more than a page per lesson. Most of the teachers they hire aren't certified teachers because it's a private school so they told us they need a unified, regimented curriculum to support people who have never taught before. At the same time though, they said we could trust the teachers to know their subject matter and that they only needed an outline of content to be covered with no recommended instructional strategies or resources because "we don't want to stifle our teachers' creativity by giving them anything that's too detailed."
Is this a common view point held by teachers and administrators that providing rich, creative, and detailed lesson plans, activities and games promotes laziness and stifles creativity? It's hogwash! I am inspired by innovative and engaging ideas that I find in other people's lessons and the more detailed they are, the easier they are for me to adapt, to understand, or to use to help my students learn. The richer my materials, the more freedom I have to experiment. The more time I have to think about how to engage particular students. When I share my lessons I get feedback on what worked and what didn't and I become a better teacher. I can't believe how entrenched this miserly attitude is about sharing materials. This curriculum meeting was composed of dozens of teachers and administrators from all over California, New York and New Jersey and they accepted this rationale without question. That we should keep the good ideas secret to try to force other people to come up with their own good ideas. Don't they know that good ideas mate with other good ideas to produce litters of new, bouncing, energetic good ideas?
And so what if you give a lazy teacher your lesson plan. Isn't that a good thing? Those kids in the lazy teacher's classroom maybe haven't encountered innovative teaching strategies before and if a lazy teacher uses someone else's lesson plan to good effect with their students, isn't that what we all want? That even kids who have "burned out" teachers have access to rich educational experiences? Why save the good teaching just for the students who happen to have been placed in your classroom? It's so silly to hoard! I guess I can understand not wanting someone to get credit for your idea, but in the end aren't we in this business to help students learn, not to accumulate "credit" for ourselves? I'm probably way too idealistic for this world. I guess I feel so strongly about this because I wouldn't be a sixth of the teacher I am today if I hadn't ripped, stolen, copied, and adapted every idea I could skim off of other teachers' blogs and websites. So I guess I am one of the lazy teachers but boy am I a better person and a better teacher for being willing to learn from all these amazing experts surrounding me.
Monday, July 8, 2013
The Logic of Geometry
I've noticed a distinct void in the Common Core where geometric logic used to have a home. This makes me really sad for three reasons:
Below are my three logic lessons if you'd like to take a look. I'm writing lessons for the other math teachers in my school so the notes are kind of overly detailed. Also my school gives us only 50 hours a year (as opposed to the usual 150-180) to get through a year's worth of material, so it's all super condensed. I don't know if it's usable outside my school, but feel free to steal and I'd love feedback. I've uploaded the pdfs below to preserve formatting but the .docx are also available on Scribd.
Note: I borrowed some of the homework problems from Harold R. Jacob's Geometry: Seeing, doing and understanding 2nd ed. and from AMSCO's Geometry. I also totally stole the formatting from Dan Wekselgreene.
- I think it's a really great way to show students how mathematical thinking can be applied to real life
- I was skipped past geometry in high school and when I got to college, the lack of logic training was a real handicap
- And I've developed a tiny bit of skepticism about Common Core. Not a lot, but I read this article about how the Common Core was developed and it creeped me out a little. The fact that only one teacher helped develop the Common Core seems kind of terrible. I recently made friends with an economics blogger and he told me that every profession engages in "turf defending" where those in the profession reject outsiders' perspectives. That immediately made me not want to be a turf defender. I won't be the person who stomps on the school house floor and screams "MINE!" Of course I want outside input, but can I also add that it's maybe a little out of hand in education? I want to teach logic damn it!
- Oh, also, I've found logic very challenging to teach and to give up on trying to find the perfect way to introduce it now just because Common Core gives me permission feels like a cop out. (so I am pretty selfish after all.)
Below are my three logic lessons if you'd like to take a look. I'm writing lessons for the other math teachers in my school so the notes are kind of overly detailed. Also my school gives us only 50 hours a year (as opposed to the usual 150-180) to get through a year's worth of material, so it's all super condensed. I don't know if it's usable outside my school, but feel free to steal and I'd love feedback. I've uploaded the pdfs below to preserve formatting but the .docx are also available on Scribd.
Note: I borrowed some of the homework problems from Harold R. Jacob's Geometry: Seeing, doing and understanding 2nd ed. and from AMSCO's Geometry. I also totally stole the formatting from Dan Wekselgreene.
Sunday, June 30, 2013
One-to-one
My school teaches students in a one-to-one classroom; one teacher, one student. Doesn't this sound awesome? From the teaching perspective, you can customize every lesson to the student and be sure they're really learning. From the student perspective, you won't have to sit while the teacher's instruction outpaces your focus or interest.
We had an IEP meeting for one of our students and we were trying to convince the local school board that this student was making dramatic progress with us and thus his needs were being met. The moderator said "who wouldn't make progress in a one-to-one classroom!" And this got me thinking. I wouldn't. I would have HATED a one-to-one environment as a student. I didn't like to be the object of too much intense teacher concentration (and really, we can be overly intense sometimes). I liked to sit back and evaluate what the teacher said before deciding to accept or reject it. I liked to have a little freedom and control over how I took my notes and whether or not my mind drifted during class. I liked the opportunity to work with other students- our collective energy was so much more powerful than mine alone.
As a teacher, I'm not a huge fan of one-to-one either. First of all, while "classroom management" is easier (this is a pretty silly word to use for one-to-one) it can also be more difficult because there's no escaping personality conflicts. It's easier to get locked into battles of will (I avoid these like I would avoid Mexican food in NY- sorry guys, it's terrible) but I've noticed these types of intense, pride posturing battles in classrooms near mine. There are no other students near by to say "hey dude, chill out" and there's no one the teacher can turn to to exchange a sympathetic look with or to share a joke with to relieve the tension. This leads to my biggest complaint against one-to-one. It assumes that the teacher can teach all the student needs to learn. THIS ISN'T TRUE! Students learn so much more from each other. The teacher can present content and establish a respectful and fun classroom culture, but the students sustain the culture, teach each other how to act, give each other support and encouragement, joke to relieve tension, boredom or frustration, and reinterpret the content in different ways so that their classmates can see it from multiple perspectives. Learning is both a solitary and group endeavor.
So I know not many people have one-to-one classroom environments so this doesn't really matter to many besides me BUT I've been reading a little bit about the advent of personalized learning software. It seems that since the whole constructivist approach to teaching math, where everyone had to learn everything in groups, hasn't really shown huge gains, there's a movement to go in the opposite direction. Personalized learning software seems like it's going somewhere. Knewton, a personalized learning software developer based in NY, and Pearson are teaming up to bring customized, competency-based learning to as many students as possible. I think their vision of the future will be students sitting at home, in coffee shops, in libraries or even in classrooms, logging in to their program and getting a wholly customized learning experience. The Knewton software amasses student data and has an algorithm that decides when a student is ready to move on to new material, and what that new material will be. This is exactly like what I'm doing right now, except without the teacher.
Here's what I see happening:
We had an IEP meeting for one of our students and we were trying to convince the local school board that this student was making dramatic progress with us and thus his needs were being met. The moderator said "who wouldn't make progress in a one-to-one classroom!" And this got me thinking. I wouldn't. I would have HATED a one-to-one environment as a student. I didn't like to be the object of too much intense teacher concentration (and really, we can be overly intense sometimes). I liked to sit back and evaluate what the teacher said before deciding to accept or reject it. I liked to have a little freedom and control over how I took my notes and whether or not my mind drifted during class. I liked the opportunity to work with other students- our collective energy was so much more powerful than mine alone.
As a teacher, I'm not a huge fan of one-to-one either. First of all, while "classroom management" is easier (this is a pretty silly word to use for one-to-one) it can also be more difficult because there's no escaping personality conflicts. It's easier to get locked into battles of will (I avoid these like I would avoid Mexican food in NY- sorry guys, it's terrible) but I've noticed these types of intense, pride posturing battles in classrooms near mine. There are no other students near by to say "hey dude, chill out" and there's no one the teacher can turn to to exchange a sympathetic look with or to share a joke with to relieve the tension. This leads to my biggest complaint against one-to-one. It assumes that the teacher can teach all the student needs to learn. THIS ISN'T TRUE! Students learn so much more from each other. The teacher can present content and establish a respectful and fun classroom culture, but the students sustain the culture, teach each other how to act, give each other support and encouragement, joke to relieve tension, boredom or frustration, and reinterpret the content in different ways so that their classmates can see it from multiple perspectives. Learning is both a solitary and group endeavor.
So I know not many people have one-to-one classroom environments so this doesn't really matter to many besides me BUT I've been reading a little bit about the advent of personalized learning software. It seems that since the whole constructivist approach to teaching math, where everyone had to learn everything in groups, hasn't really shown huge gains, there's a movement to go in the opposite direction. Personalized learning software seems like it's going somewhere. Knewton, a personalized learning software developer based in NY, and Pearson are teaming up to bring customized, competency-based learning to as many students as possible. I think their vision of the future will be students sitting at home, in coffee shops, in libraries or even in classrooms, logging in to their program and getting a wholly customized learning experience. The Knewton software amasses student data and has an algorithm that decides when a student is ready to move on to new material, and what that new material will be. This is exactly like what I'm doing right now, except without the teacher.
Here's what I see happening:
- computers probably aren't smart enough to do this yet. I don't know if they ever will be. I have an Algebra student who asked me if numbers go on forever. We had a nice side discussion on the nature of number and infinity which he understood. His abstract reasoning capabilities have far outpaced his computational competence so he asks really good, deep math questions and understands the answers even when he struggles with adding fractions. I can satisfy his deeper curiosity while still drilling him on basic arithmetic. A program would decide that he's not ready for anything beyond basic computation.
- I do believe that school is about more than learning content. I think that learning to work cooperatively is important. Learning to share a joke to relieve stress is important. Learning how to speak up for yourself to an authority figure is important. Socialization is important. Maybe this just makes me old fashioned. But having people by your side makes learning more fun too.
- Peers push you to accomplish more than you can by yourself. This is a problem I've seen in one-to-one teaching- that it's so much harder to motivate a student to study independently or to work on projects. When there's no one to share it with, no peer audience, teenagers shut down and disengage. Duh! Even teenagers with special needs (we teach a lot of students with severe social anxiety) need peers to support them. Even if you place kids in the same classrooms to use these educational technologies, they won't be learning the same content so won't be able to support or motivate each other effectively.
- Finally, if you allow students to do the work at home, I think cheating will become the norm. I think it already is. A coworker of mine (a teacher!) admitted to me that she takes all of her sisters' online tests for her because her sister is an athlete and doesn't need school.
Can't we find a middle ground? There is never going to be one model that works for everyone, but we all deserve to experience different types of learning. I may not like one-to-one learning because it makes me uncomfortable, but I went in to see my professors to get help on papers and it was good for me. We all need a mix of different experiences. We need technology and classrooms and individualized instruction and games and textbooks and teachers. Why can't technology make our classrooms richer and more full of different kinds of learning? Why is it a choice between classrooms or personalized learning? Can't we recognized that there are good things about classrooms? Why are we so obsessed with "or"? Why not and? Knewton and Pearson might say though that they are offering an "and" option. That this is meant to enrich teachers' curricula not replace them, but I'm suspicious that this is just another way to devalue teachers' professionalism. I read an article in Newsweek (I think but of course I can't find it now) where the head of one of these personalized software companies admitted that he didn't employ any educators on staff. And Pearson, based on what I've seen of their textbooks, doesn't know that much about teaching either.
Saturday, February 2, 2013
Logarithm Dominoes
I'm currently planning my pre-calc unit on logarithms and I just can't seem to find enough fun ways to drill logarithms. It really is just about practice I think, but I HATE giving students worksheets full of problems. I groan every time I see a Kuta software worksheet. I know that games basically just do the same thing in a dressed up form, but at least there's a measure of competition or strategy that gives students a focus. I just read Amy Gruen's post on practicing logarithms and almost threw out some expletives because I saw her link to logarithm dominoes and I spent a nice chunk of time last weekend to making my own logarithm dominoes. Its both wonderful and incredibly frustrating to spend hours on something then find that someone got there first and did it better. At least you know your idea was good, but you could have saved yourself so much time! (this happened to me last year with Kate Nowak's logarithm laws worksheet . I'd made one for myself then stumbled upon hers and hers was so much better!) But fortunately for me, Amy Gruen's logarithm dominoes are very different from mine, so I thought I'd share what I came up with.
I threw together the following logarithm property dominoes. I haven't had a chance to try them out yet, so I'm not sure the ratios are correct. But I figured it was a start and I don't know when I'll have the initiative or time to post them again. Here are the dominoes:
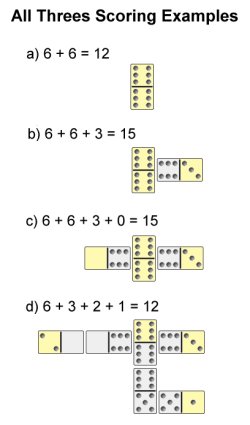
You should be able to play any domino game with these cards that you want but I planned to play the game "all threes". Here are the rules:
I threw together the following logarithm property dominoes. I haven't had a chance to try them out yet, so I'm not sure the ratios are correct. But I figured it was a start and I don't know when I'll have the initiative or time to post them again. Here are the dominoes:
You should be able to play any domino game with these cards that you want but I planned to play the game "all threes". Here are the rules:
- Each player draws 5 dominoes. You start by playing a double domino (one end equals the same number as the other end: 2-2 for example)
- You can build off the double domino in 4 directions- above, down, left and right. To play off a domino, you must match ends that have the same value.
- Players take turns placing dominoes.
- If a player can’t place a domino, they must draw more dominoes until they can play.
- After each player places a domino, count up the total of all loose ends. If the total is a multiple of 3, the player gets that many points.
- The game ends when either a player runs out of dominoes in their hand or when a player reaches 100 points. If a player runs out of dominoes in their hand, the player with the most points wins.
Since these are logarithm expressions and not straight forward pips, players must make the conversions in their
head or on paper.
Now I just need to figure out a fun way to teach solving logarithm and exponential equations....
Labels:
dominoes,
games,
logarithm properties,
logarithms,
Pre-calculus
Subscribe to:
Posts (Atom)